Take Part in the Data Revolution
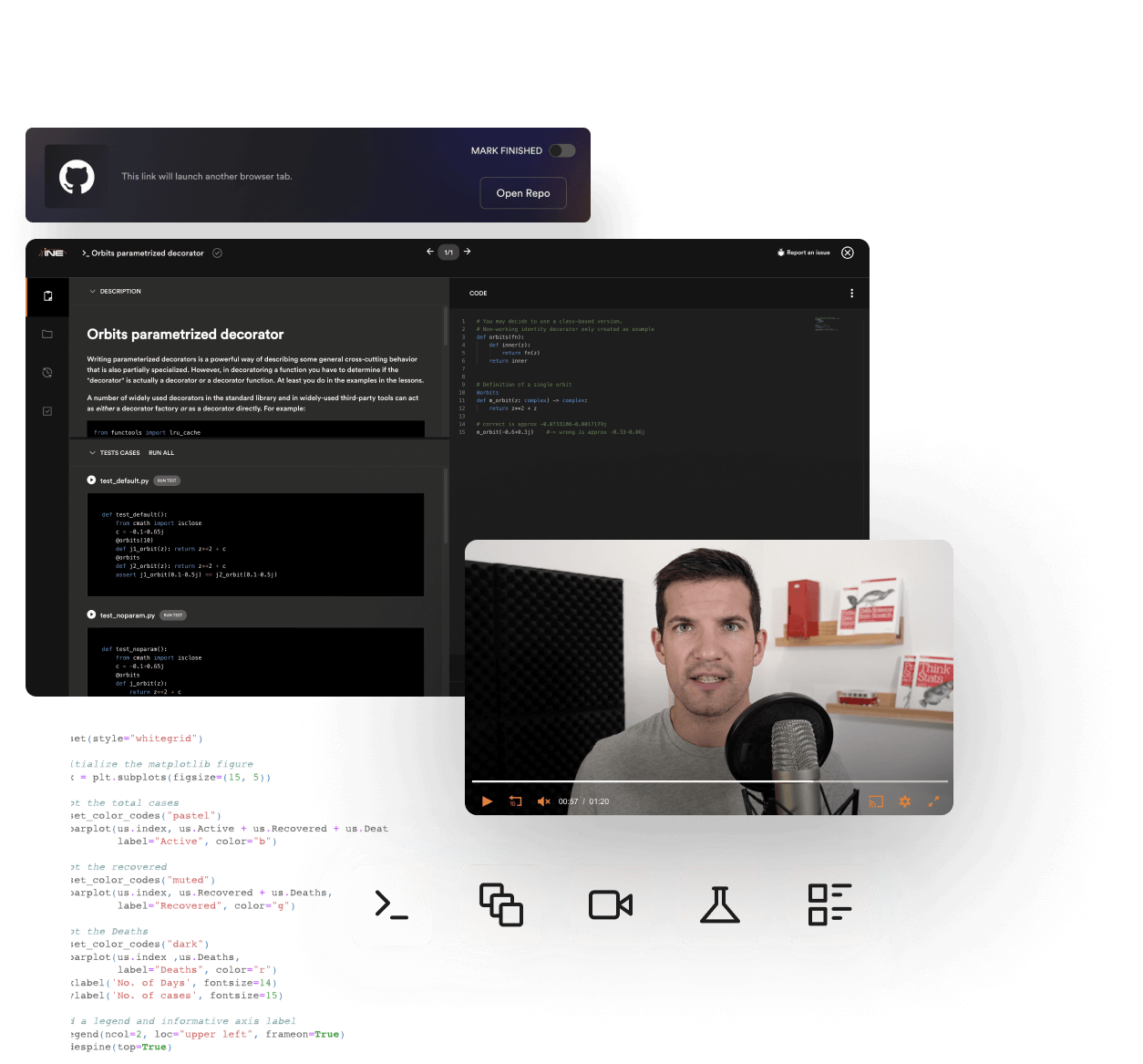
Become an Active Participant in Your Education
We’ve got Data Science training down to a science. Regardless of your preferred programming language or proficiency in deep learning frameworks, our hands-on, interactive training material is designed for all levels and styles of learning.
Train at your own pace with extensive, on-demand video courses led by expert Data Scientists utilizing Jupyter Notebooks designed to guide you through the content. Each video is built upon core objectives, community observations, and the experiences of your instructor, blending concrete information with real-world scenarios. Once you’ve learned your skills, you can put them to the test through hands-on, interactive Python and Data Analytics courses paired with real-time feedback and experience-building Github projects.
Data Science is one of the most rapidly evolving fields in information technology, with an estimated 31% growth rate. Now is the time to add value to your team and your organization through expert-led training. Whether you want to continually develop your analysis skills or perfect your programming abilities, our platform is the most comprehensive and in-depth learning resource available. Get started today.
Data Science Learning Paths
Learning Paths, designed to keep every crucial topic in one place, guide you through the study process. Each course is organized within the Learning Path for efficiency, focus, and retention. The only thing you have to keep track of is your accomplishments.
Start your training today! Explore hundreds of hours of course materials.
Choose the training you want from our library of over 250+ hours of completely original content and get hands-on with INE quizzes, GitHub projects, and programming exercises to reinforce your knowledge through a practical approach to learning.
What a Data Science career looks like
Data science is not only a rapidly growing field, but an exciting one filled with opportunity. Data scientists work with every major industry and are shaping the future for businesses around the world.

Data Analyst
A Data Analyst uses data to acquire information about specific topics. This may involve finding survey participants, gathering data, interpreting data, and then presenting it in forms such as charts or reports.

Data Scientist
Data Scientists are responsible for mining complex data and designing new ways to manage statistical data using models.

Data Engineer
Data Engineers are responsible for developing and translating computer algorithms into code. They are also responsible for maintaining, organizing, and identifying trends in large data sets.

Data Architect
A Senior Software Engineer usually has a strong background in computer science, web development, and/or engineering. Knowledge and familiarity with web coding such as Javascript, HTML, and CSS are a necessity.
Data Science Certifications
Learn from our experts!
The best way to become an expert is to learn from one! Our training materials are produced entirely in-house by INE instructors who are some of the most respected and tenured experts in the industry.
Alexis Perrier
Author @ Packt Publishing Data Science Consultant PhD Signal Processing
David Mertz
Ph.D. Philosophy
Adriana Patterson
Data Science
Common questions about Data Science training
If you have a question you don’t see on this list, please visit our Frequently Asked Questions page by clicking the button below. If you’d prefer getting in touch with one of our experts, we encourage you to call one of the numbers above or fill out our contact form.
What are the most in-demand programming languages?
How do I start a Data Science career?
/ LET’S GET IN TOUCH
Have a question? We’re here to help!
Whether you’d like more information on our training materials or are interested in a free demo, please contact us at any time.
Monday - Friday8:00 AM - 5:00 PM Eastern Time
US Customer1-877-224-8987
Outside US+1-984-444-9917
Sales Emailinfo@ine.com
Support Emailsupport@ine.com